Options are a type of financial instrument that derive their value from an underlying security. Hence, they are often known as derivatives. Before moving to financial options perhaps it will may be useful to give a simpler analogous example.
Football Cards
Example 1
Say you and a friend collect football cards, your friend has Card A and offers you the option to purchase this card at a fixed price say $100 this time next year. For this privilege your friend charges you $10. Now consider the scenarios that are possible this time next year, if Card A is now selling for $200 in the open market, you have the right to buy the card from your friend and sell it for a profit immediately. On the other hand if the card is now selling for $70 in the open market, you will just let your friend keep the card (and your $10) because if you wanted to buy it, you could get a cheaper price just buying it in the market as opposed to the $100 price you agreed to in the contract with your friend.
Example 2
Your friend just bought a brand new football card (Card B) in the open market for $1000. He is worried about the price dropping below some level in the next year, say $800. He comes to you and asks to enter a contract to buy the card from him if the price should drop below $800. You agree and tell him that this right will cost him $150. Say for instance the price of Card B is now $100, well since you entered into the agreement to buy it from your friend at a price of $800 you are now obligated to buy it from him. On the other hand if the price is now $1100 your friend clearly won't exercise his right to sell the card to you at $800 as he would get a much better price on the open market, in this case you keep the $150 he paid for entering the contract.
Example 3
There is a card in the market (Card C) that neither you nor your friend own. You want to enter into a contract for the right to buy the card 6 months from now. Since the value of such a contract is derived your friend doesn't actually have to own the card to enter the contract. Although think on this for a while, say the card is selling for $10 now, and your friend agrees to this contract at $3, your friend will be liable to pay you a potentially infinite sum should the price of the card increase dramatically.
So what's important to note here is that the creation of an option on one side creates an obligation on the other. The party with the obligation is known as the writer of the option. So in example 1 your friend is the writer whereas you are the buyer, you have the optionality and he has the obligation. The opposite is true for example 2, in that you are obligated to buy the card from your friend if he exercises his option. Since an option derives its value from an underlying asset the writer of the option doesn't actually have to own the underlying asset to write the option. Clearly there is increased risk with this approach known as writing a naked option.
The idea here is that an option can be on anything as long as there are two parties willing to enter the agreement.
Types of Options
Call option
A call option is the right to buy an asset at a predetermined price. Example 1 we give above is a call option as it gives the holder the right to buy.
Put Option
A put option is the right to sell and asset at a predetermined price. Example 2 is a put option contract.
European Option
In the examples we gave above, the option holder only had the option to exercise the right to buy/sell the card on a fixed date. Take example 1, say in one week from now the price increases to $150 , clearly this is in your (option holder) favour. However, you don't have the right to buy the option from your friend yet, as the contract specifies that you are only allowed to exercise it one year after the contract is created. So if the price drops back down on the expiration day, you can only get that price on that day. This is known as a European option.
American Option
An American option gives the holder the write to buy the option at any time over the life of the option. Take example 1 again and assume that 1 day after creating the contract the price of the card doubles, you now have the right to exercise the option if you so wish, you also have the option to hold on to it and wait to exercise it at any time over the life of the option. Clearly the American option gives the holder more optionality. Consider if you were presented with two choices, one an American option and the other a European, clearly you would be willing to pay more for the American version since it offers more opportunities.
See this interesting discussion on the origins of the two terms.
Stock Options
A stock option acts the same as the football card example we have described above, the only difference is that the underlying asset is a stock. Let's take a few quick examples:
Example 1 Long Call
A stock is currently trading at $50, there is also an option to buy this stock 3 months from now, this option costs $10 and gives the holder the right to buy the stock at $55. You buy this option and in 3 months time the stock is currently trading at $65. So you now have the right to buy the stock at $55. In this case it is in your interest to exercise the option since it is profitable to do so.
Let's put some notation to these concepts which will become important later on.
\(T = \text{Time in years until contract can be exercised (0.25 in this case)}\)
\(S_0 = \text{Price of stock at this moment (50 in this case)}\)
\(K = \text{Price you agree to buy or sell at (55 in this case) known as strike price}\)
\(S_T = \text{Price of stock (65) at time T (0.25) }\)
\(C = \text{Price of the call option (10 in this case)}\)
Payoff from option in this case = \(S_T - K = 65 - 55 = 10\)
Profit in this case is \(S_T - K - C = 65 - 55 - 10 = $0\)
Long call payoff
The general formula for buying a call option, known as long call is as follows:
\(\text{Long call payoff} =max(S_T - K, 0)\)
Long call profit
The general formula for the profit from buying a call option is given below.
\(\text{Long call profit} = max(S_T - K, 0) - C\)
Why is max included in the above formulae? Well, this is the mathematical representation of not exercising the option if it is not in your favour to do so. Say for example you could get a better price on the open market, there is no reason to buy at the price stipulated in the contract.
Long Call Breakeven Price
The breakeven price is the price at which the overall profit from entering the position is 0. So if we think about that for a little while, we will realize, it is the future asset price - strike price such that the payoff equals the premium. Or just strike + premium. In our example this would be 55 (K) + 5 (C) = $60. So anything above/below $60 we are in profit/loss.
\(\text{Breakeven} = K + C\)
Plotting Long Call Payoff Diagram
Take an example where the price of the options is $5 and the strike is $55. Notice below that the difference between the payoff line and the profit line is always a constant value of the price of the option C ($5 in this case). Anything to the right of the breakeven price (dashed line) will result in profit for the holder, whereas anything to the left results in loss, although this loss is bounded at the cost of the option $5 in this case. Also note the infection point on the black line, this represents the point at which we will exercise the option. Say for example the price at time T is $56, we would still exercise here as we would recoup $1 for a loss of $4 as opposed to a loss of $5.
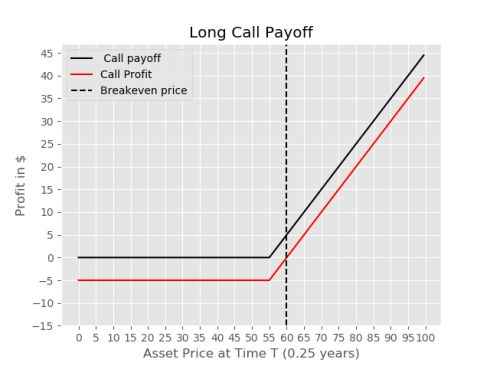
Example 2 Long Put
A stock is currently trading at $100, there is also an option to sell this stock 1 .5 years from now at $90, it costs 30$ to purchase this put option, you buy this option and in 1 year the price of the stock is $100. In this case you would not exercise the option, since you can sell the stock in the market at a higher price.
\(T = \text{Time in years until contract can be exercised (1.5 in this case)}\)
\(S_0 = \text{Price of stock at this moment (100 in this case)}\)
\(K = \text{Price you agree to buy or sell at (90 in this case)}\)
\(S_T = \text{Price of stock (110) at time T (1.5) }\)
\(P = \text{Price of the put option (30 in this case)}\)
Payoff from option in this case \(max(K - S_T,0) = max(90-110, 0) = 0\)
Profit in this case is -$30 (price we paid for the option)
Long Put Payoff
The general formula for a long put position's payoff function is given below.
\(\text{payoff}= max(K- S_T, 0 )\)
As with the long call payoff and profit functions the max in the formulae above indicates the decision point where at which we do not exercise the option.
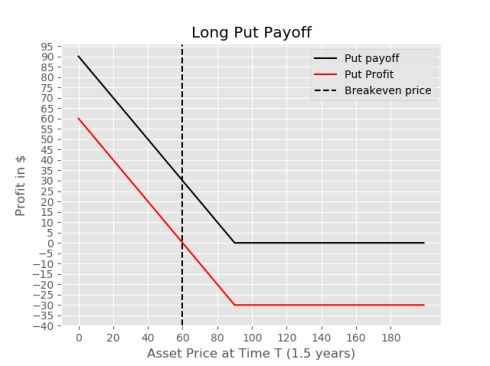
Plotting Long Put Payoff Diagram
The diagram for the payoff and profit from a long put position is given below, here the potential profit is limited to the strike price - put premium, in this example the maximum potential profit would be $60 which would be realized if the stock price was 0 in 1.5 years. As with the long call option, entering a long put limits the downside risk for the holder to no more than the premium it costs to enter the position. The values to the left of the infection point on the payoff line represent prices at which we exercise the option.
Example 3
You sell a call option for 20$ that gives the holder the right to buy a stock at $100 in 6 months time, the stock is currently selling for $110 in the market. If the stock is priced at $160 for example on the date of expiry you are forced to sell to the option holder for $100. This is an obligation not an option! It is important to note here that your losses are potentially unlimited when writing a call option.
\(T = \text{Time in years until contract can be exercised (0.5 in this case)}\)
\(S_0 = \text{Price of stock at this moment (110 in this case)}\)
\(K = \text{Price you agree to buy or sell at (100 in this case) known as strike price}\)
\(S_T = \text{Price of stock (110) at time T (0.5) }\)
\(C = \text{Price of the call option (20 in this case)}\)
Payoff from option in this case = \(-(S_T - K) = -(160 - 100) = -60\)
Profit in this case is \(S_T - K + C = -(160-100) +20 = -$40\)
Rather than provide formulae for the payoff and profit we can realize that since an option is a two way contract, the payoff and profit for selling a call option can be thought of simply as a vertical reflection of the long call. So all we would need to do in this case is take the negative of a long call payoff / profit and this will give us the payoff/profit for a short call. This makes sense intuitively also, since an options contract requires two parties, one with an obligation and the other with an option, profit for the writer is a loss for the seller and vice versa.
The breakeven price for a short call is also the same as it is for a long call K + C.
Let's take a look at the payoff diagram for a short call.
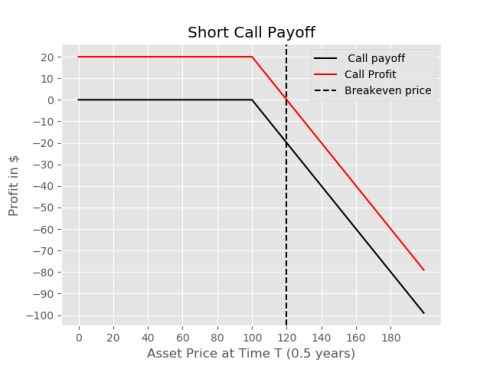
The potential profit from entering this position is capped at the premium, whereas the potential losses are unbounded.
The vertical reflection we mentioned earlier, is depicted below, this should illustrate the relationship between a short and a long call option position. Essentially they are just the opposite of eachother.
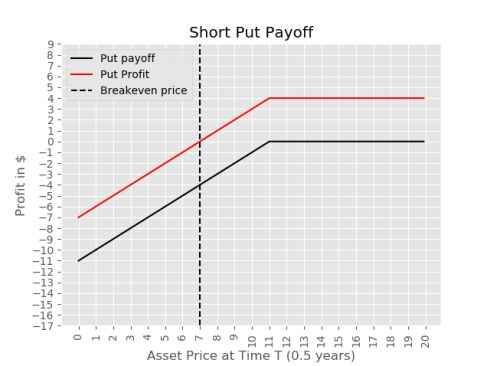
Example 4: Short Put Payoff
A stock is currently trading at $10, there is also an option to sell this stock 6 months from now at $11, it costs 4$ to purchase this put option, you sell this option and in 6 months the price of the stock is $5. In this case you would be liable to buy the stock from the option holder at $11.
\(T = \text{Time in years until contract can be exercised (0.5 in this case)}\)
\(S_0 = \text{Price of stock at this moment (10 in this case)}\)
\(K = \text{Price you agree to buy or sell at (11 in this case)}\)
\(S_T = \text{Price of stock (5) at time T (0.5) }\)
\(P = \text{Price of the put option (4 in this case)}\)
Payoff from option in this case \(-max(K - S_T,0) = = max(11-5, 0) = -6\)
Profit in this case is -$30 (price we paid for the option)