What is a Set?
In Python, a set is an unordered collection of unique elements. It is defined by enclosing elements within curly braces {}. Sets do not allow duplicate values, so any repeated elements in a set will be automatically removed. They support various mathematical operations like union, intersection, and difference, making them useful for handling distinct data and performing set-related computations efficiently. The main characteristics of sets are their uniqueness and the lack of a specific order for elements, distinguishing them from other collection types like lists and tuples.
We will take 2 sets as examples to work with throughout this article. Note that items contained within sets are known as elements which is the same terminology as discussed with lists here.
# Sample elements for sets A and B
set_A = {1, 2, 3, 4, 5}
set_B = {3, 4, 5, 6, 7}
Indexing a Set Element
A set is not able to access an element by index in the way a list is. If a user attempts this python will return an error.
set_A = {1, 2,3, 4, 5}
set_A[1]
Will return the error shown below
TypeError: 'set' object is not subscriptable
Add Element to a Set
Consider this addition to a set example: we have a set named set_A, which already contains the elements {1, 2, 3, 4, 5}. Now, we attempt to add the element 2 to set_A, but it remains unchanged. Why? Because sets only allow unique elements, and since 2 is already a member of set_A, adding it again has no effect as it remains a unique collection of elements.
set_A = {1, 2, 3, 4, 5}
set_A.add(2)
print(set_A)
'''
{1, 2, 3, 4, 5}
'''
Observe what happens when we add an element that is not already in the set. As expected it is added as a new element within set_A.
set_A = {1, 2, 3, 4, 5}
set_A.add(0)
print(set_A)
'''
{0, 1, 2, 3, 4, 5}
'''
Remove from a Set
Removing an element from a set works in the same way as removing an element from a list. We simply use the set_name.remove(element) syntax.
set_A = {1, 2,3, 4, 5}
set_A.remove(2)
print(set_A)
'''
{1, 3, 4, 5}
'''
Operations Between Two or more Sets
In order to understand operations between two or more sets, take the following diagram , known as a Venn Diagram
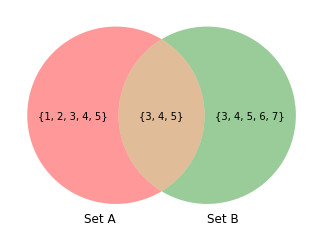
Our sets A and B are represented above as red and green circles respectively.
Set Intersection
A set intersection represents the elements that are common across two or more sets. This would represent the brown shaded region in the diagram above. In mathematics this is given the symbol \(\cap\) to represent the intersection operation. A python example of taking the intersection between our sets \(A \cap B\) is shown below. The intersection method is how python knows we want to take the elements that are in both sets
set_A = {1, 2, 3, 4, 5}
set_B = {3, 4, 5, 6, 7}
print(set_A.intersection(set_B))
'''
{3, 4, 5}
'''
Note that we can obtain the same results if we were to take the intersection of A with B as B with A or \(A \cap B \text{ is equivalent to } B \cap A\)
set_A = {1, 2, 3, 4, 5}
set_B = {3, 4, 5, 6, 7}
print(set_A.intersection(set_B) == set_B.intersection(set_A))
'''
True
'''
So it is import to note that the set_intersection() method returns a new set.
Set Union
The union operator given the \(\cup\) symbol in mathematics is used to denote the addition of two sets. As mentioned previously sets contain distinct elements. We can think of a set union as taking the green and the red shaded parts and adding them together. First let us try that from scratch using only the add() method.
set_A = {1, 2, 3, 4, 5}
set_B = {3, 4, 5, 6, 7}
set_A.add(3)
set_A.add(4)
set_A.add(5)
set_A.add(6)
set_A.add(7)
print(set_A)
'''
{1, 2, 3, 4, 5, 6, 7}
'''
We can get the same result by using the union method directly on either set.
print(set_A.union(set_B))
'''
{1, 2, 3, 4, 5, 6, 7}
'''
Set Difference
This can be though of as taking Set A (red circle) and removing the intersection (shaded brown region)
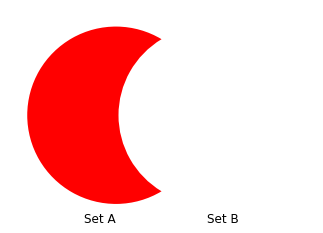
Taking the difference between two sets is equivalent to removing the elements of one set that are also elements in another. Let's see an example using only the remove method to take set A - set B
set_A = {1, 2, 3, 4, 5}
set_B = {3, 4, 5, 6, 7}
set_A.remove(3)
set_A.remove(4)
set_A.remove(5)
print(set_A)
'''
{1,2}
'''
If we were to try to remove say set_A.remove(6) , python would return KeyError: 6 , meaning we are trying to remove an element that is not present in the set.
We will get the same result using the difference() method directly on set A and passing set B as an argument
set_A = {1, 2, 3, 4, 5}
set_B = {3, 4, 5, 6, 7}
print(set_A.difference(set_B))
'''
{1, 2}
'''
Set Symmetric Difference Method
The symmetric difference operator can be thought of as taking the elements of A and elements of B and removing the intersection. So from the initial diagram that would mean the red plus the green minus the brown. We can also think of this as the union of A and B minus the intersection.
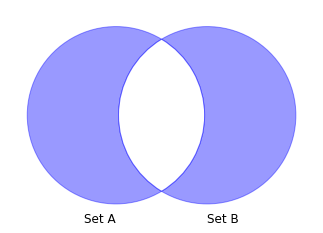
We can take the symmetric difference of two sets by using the symmetric_difference method on a set and passing another set as an argument.
set_A = {1, 2, 3, 4, 5}
set_B = {3, 4, 5, 6, 7}
print(set_A.symmetric_difference(set_B))
'''
{1, 2, 6, 7}
'''